【C++】二叉搜索树

文章目录
- 一、概念与性能分析
- 二、二叉搜索树的实现
- 1. 结点
- 2. 默认成员函数
- 3. 插入
- 4. 查找
- 5. 删除
- 6. 中序遍历
- 7. 完整实现
- 三、key和key/value
一、概念与性能分析
二叉搜索树,又称搜索二叉树、二叉排序树,是一种具有特殊性质的二叉树:
- 左子树上所有结点的值都小于等于根结点的值
- 右子树上所有结点的值都大于等于根结点的值
- 它的左右子树也都是二叉搜索树
- 二叉搜索树中可以支持插入相等的值,也可以不支持插入相等的值,具体看场景需求
由于它本身和它的子树都是二叉搜索树,不难想象:二叉搜索树的中序遍历一定是升序序列
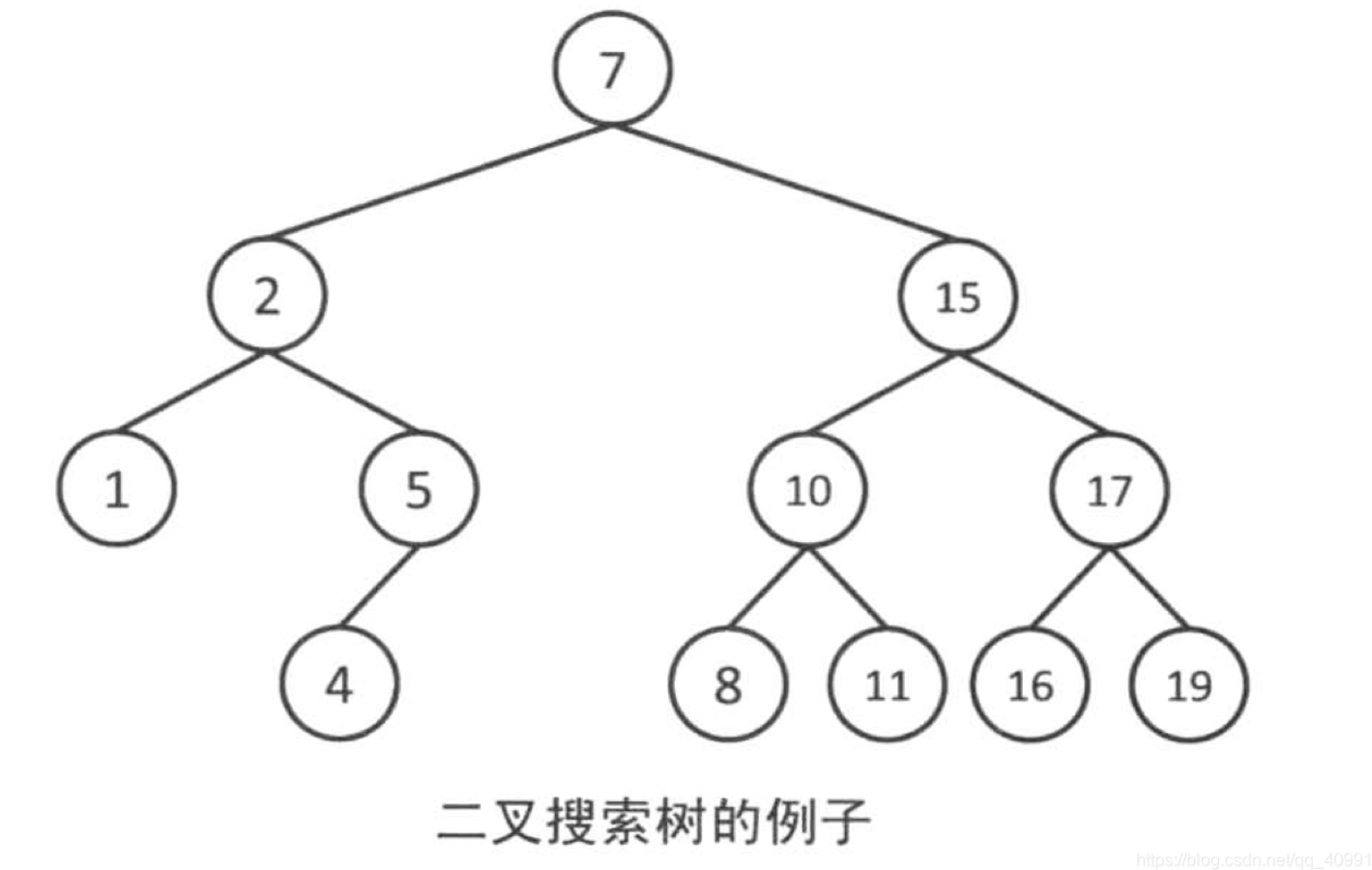
从名字就能看出来,二叉搜索树主要用于搜索。最优情况下,如果它接近完全二叉树的结构,不难分析,最大搜索次数即其树的高度:log2N;最差情况下,如果它接近单支树的结构,则其搜索次数接近结点个数:N。
所以综合来看二叉搜索树的增删查改效率为O(N),这样的时间复杂度还是太高了。必须将二叉搜索树的结构进一步优化,也就是以后要学习的平衡二叉搜索树AVL树、红黑树。
二、二叉搜索树的实现
1. 结点
首先需要定义出结点的结构:
template<class K>
struct BSTreeNode
{BSTreeNode* _left;BSTreeNode* _right;K _key;BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key){ }
};
2. 默认成员函数
由于树的类中涉及到结点资源的开辟和删除,所以需要我们自己写拷贝构造、赋值重载、析构函数等。
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
private:Node* _root;public:
//......
}
- 默认构造函数:
//默认构造一棵空树
BSTree():_root(nullptr)
{ }
之前我们学习链式结构的树,它的很多操作都需要用递归完成,但我们这里的拷贝构造、析构函数没办法传参递归怎么办?我们可以写出递归的函数后,“包装”起来:
- 拷贝构造函数:
BSTree(const BSTree<K>& t)
{//实际完成拷贝功能的是Copy函数,我们的拷贝构造只是把他包装起来_root = Copy(t._root);
}Node* Copy(Node* root)
{if (root == nullptr){return nullptr;}Node* newnode = new Node(root->_key);//利用递归完成所有结点的拷贝newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);return newnode;
}
- 析构函数:
~BSTree()
{Destory(_root);_root = nullptr;
}void Destory(Node* root)
{if (root == nullptr){return;}//利用递归完成所有结点的资源释放Destory(root->_left);Destory(root->_right);delete root;
}
拷贝构造函数的Copy函数和析构函数的Destory函数仅供它们内部使用,所以可以把它们放到private部分
- 赋值运算符重载:
BSTree<K>& operator=(BSTree<K> t)
{swap(_root, t._root);return *this;
}
3. 插入
二叉搜索树的插入要按照搜索树的性质寻找正确位置插入:
- 树为空,则直接新增结点作为root
- 树不为空,则按照二叉搜索树性质,插入值比当前节点值大就往右走,插入值比当前节点值小则往左走。直到找到空位置,插入新节点:

代码实现:
bool Insert(const K& key)
{if (_root == nullptr){_root = new Node(key);return true;}//parent保存待插入位置的父结点Node* parent = nullptr;Node* cur = _root;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{//如果key值已存在,则插入失败return false;}}//cur找到了正确的位置cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;
}
4. 查找
查找一个值是否存在,也很简单了:
bool Find(const K& key)
{Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else //key == cur->_key,找到了{return true;}}return false;
}
5. 删除
二叉搜索树的删除相对复杂,首先查找待删除元素结点,不存在则返回false。
若存在,则显然有以下几种情形:(假设要删除的结点为x)
x没有孩子、有左孩子或右孩子、有两个孩子。
为了删除结点后不破坏搜索二叉树的性质,它们要用不同的解决方法:
- 若x没有孩子,则直接删除x
- 若x只有一个孩子,则让x的父亲的原指向x的指针改为指向x的孩子,再删除x
- 若x有两个孩子,使用替换法:找x的左子树的最大结点l(即左子树的最右结点),或x的右子树的最小结点r(即右子树的最左结点),代替x。因为这两个结点的值替换x后,都还能保持搜索二叉树的性质。最后再删除l或r结点,因为l或r结点一定是没有孩子或只有一个孩子的,再用上面两种情形方法处理就好。



代码实现,可以将情形1和情形2整合讨论:
bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else //找到了待删除结点cur,开始删除{//如果cur左孩子为空,就连接parent和cur的右子if (cur->_left == nullptr){//特殊情况cur为根结点,cur右孩子当根结点if (cur == _root){_root = cur->_right;}else{//如果cur是parent的左,则让parent的左指向cur的右子if (cur == parent->_left){parent->_left = cur->_right;}//如果cur是parent的右,则让parent的右指向cur的右子else{parent->_right = cur->_right;}}delete cur;}//如果cur右孩子为空,就连接parent和cur的左子else if (cur->_right == nullptr){//特殊情况cur为根结点,cur左孩子当根结点if (cur == _root){_root = cur->_left;}else{//如果cur是parent的左,则让parent的左指向cur的左子if (cur == parent->_left){parent->_left = cur->_left;}//如果cur是parent的右,则让parent的右指向cur的左子else{parent->_right = cur->_left;}}delete cur;}else //两个孩子,这里选择找左子树的最大结点替换{Node* LeftMaxParent = cur;Node* LeftMax = cur->_left;//找左子树的最右结点while (LeftMax->_right){LeftMaxParent = LeftMax;LeftMax = LeftMax->_right;}swap(cur->_key, LeftMax->_key);//此时LeftMax一定没有右孩子,可能有左孩子//还可能LeftMaxParent就是根结点,所以要判断LeftMax是其父的左还是右孩子 if (LeftMaxParent->_left == LeftMax){LeftMaxParent->_left = LeftMax->_left;}else{LeftMaxParent->_right = LeftMax->_left;}delete LeftMax;}return true;}}return false;
}
6. 中序遍历
为了验证二叉搜索树的性质,我们要判断中序遍历的结果是否是升序的:
void InOrder()
{_InOrder(_root);cout << endl;
}void _InOrder(Node* root)
{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);
}
同样地,将_InOrder函数放在private中。
7. 完整实现
综上,二叉搜索树的完整实现:
namespace lydly
{template<class K>struct BSTreeNode{BSTreeNode* _left;BSTreeNode* _right;K _key;BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key){ }};template<class K>class BSTree{typedef BSTreeNode<K> Node;private:Node* _root;public://默认构造一棵空树BSTree():_root(nullptr){ }//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}~BSTree(){Destory(_root);_root = nullptr;}bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{//如果key值已存在,则插入失败return false;}}//cur找到了正确的位置cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else //key == cur->_key找到了{return true;}}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else //找到了待删除结点,开始删除{//如果cur左孩子为空,就连接parent和cur的右子if (cur->_left == nullptr){//特殊情况cur为根结点,cur右子当根if (cur == _root){_root = cur->_right;}else{//如果cur是parent的左,则让parent的左指向cur的右子if (cur == parent->_left){parent->_left = cur->_right;}//如果cur是parent的右,则让parent的右指向cur的右子else{parent->_right = cur->_right;}}delete cur;}//如果cur右孩子为空,就连接parent和cur的左子else if (cur->_right == nullptr){//特殊情况cur为根结点,cur左子当根if (cur == _root){_root = cur->_left;}else{//如果cur是parent的左,则让parent的左指向cur的左子if (cur == parent->_left){parent->_left = cur->_left;}//如果cur是parent的右,则让parent的右指向cur的左子else{parent->_right = cur->_left;}}delete cur;}else //两个孩子,这里选择找左子树的最大结点替换{Node* LeftMaxParent = cur;Node* LeftMax = cur->_left;//找左子树的最右结点while (LeftMax->_right){LeftMaxParent = LeftMax;LeftMax = LeftMax->_right;}swap(cur->_key, LeftMax->_key);//此时LeftMax一定没有右孩子,可能有左孩子//还可能LeftMaxParent就是根结点,所以要判断LeftMax是其父的左还是右孩子 if (LeftMaxParent->_left == LeftMax){LeftMaxParent->_left = LeftMax->_left;}else{LeftMaxParent->_right = LeftMax->_left;}delete LeftMax;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void Destory(Node* root){if (root == nullptr){return;}Destory(root->_left);Destory(root->_right);delete root;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node* newnode = new Node(root->_key);//利用递归完成所有结点的拷贝newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);return newnode;}};
}
简单测试:

没有问题。
三、key和key/value
上面我们实现的二叉搜索树,结点中只存储了一个key,称为关键码,关键码即为需要搜索的值,使用这种二叉搜索树的场景只需要判断key是否存在。key的搜索场景实现的二叉搜索树支持增删查,不支持修改,因为修改key值破坏二叉搜索树性质了。
使用这种key二叉搜索树的场景,比如小区车库,只有业主的车能进入,车牌号作为key值,就在系统中检查key是否存在以确定是否为业主的车。
还有一种key/value的搜索场景:每一个关键码key,都有与之对应的value,value可以为任意类型对象,增删查还是以key为关键码在二叉搜索树中操作,修改不能改key,但是可以修改value。
使用这种key/value二叉搜索树的场景,比如英语词典,树的结构中存储key(英文)和value(中文),搜索时输入英文作为key进行查找,找到后输出对应的value中文。
key/value二叉搜索树的实现:
namespace lydly
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key; V _value; BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;private:Node* _root = nullptr;public:BSTree(){ }BSTree(const BSTree<K, V>& t){_root = Copy(t._root);}BSTree<K, V>& operator=(BSTree<K, V> t){swap(_root, t._root);return *this;}~BSTree(){Destory(_root);_root = nullptr;}bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 准备删除if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else // 两个孩子{Node* pMinRight = cur;Node* minRight = cur->_right;while (minRight->_left){pMinRight = minRight;minRight = minRight->_left;}swap(cur->_key, minRight->_key);if (pMinRight->_left == minRight){pMinRight->_left = minRight->_right;}else{pMinRight->_right = minRight->_right;}delete minRight;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}void Destory(Node* root){if (root == nullptr){return;}Destory(root->_left);Destory(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* copy = new Node(root->_key, root->_value);copy->_left = Copy(root->_left);copy->_right = Copy(root->_right);return copy;}};}
本篇完,感谢阅读。
