数论总结,(模版与题解)
数论
- 欧拉函数
- X质数(线性筛与二进制枚举)
- 求解组合数
- 欧拉降幂(乘积幂次)
- 乘法逆元
- 最小质因子之和
- 模版
欧拉函数
欧拉函数的定义就是小于等于n的数里有f(n)个数与n互质,下面是求欧拉函数的模版。

package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.Scanner;public class 欧拉函数模版 {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();for (int i = 0; i < n; i++) {int x = scanner.nextInt();System.out.println(oula(x));}}static int oula(int x){int res = x;for (int i = 2; i <= x / i; i++) {if (x % i == 0) {res = res / i * (i - 1);while (x % i == 0) {x /= i;}}}if(x > 1){res = res / x * (x-1);}return res;}
}X质数(线性筛与二进制枚举)
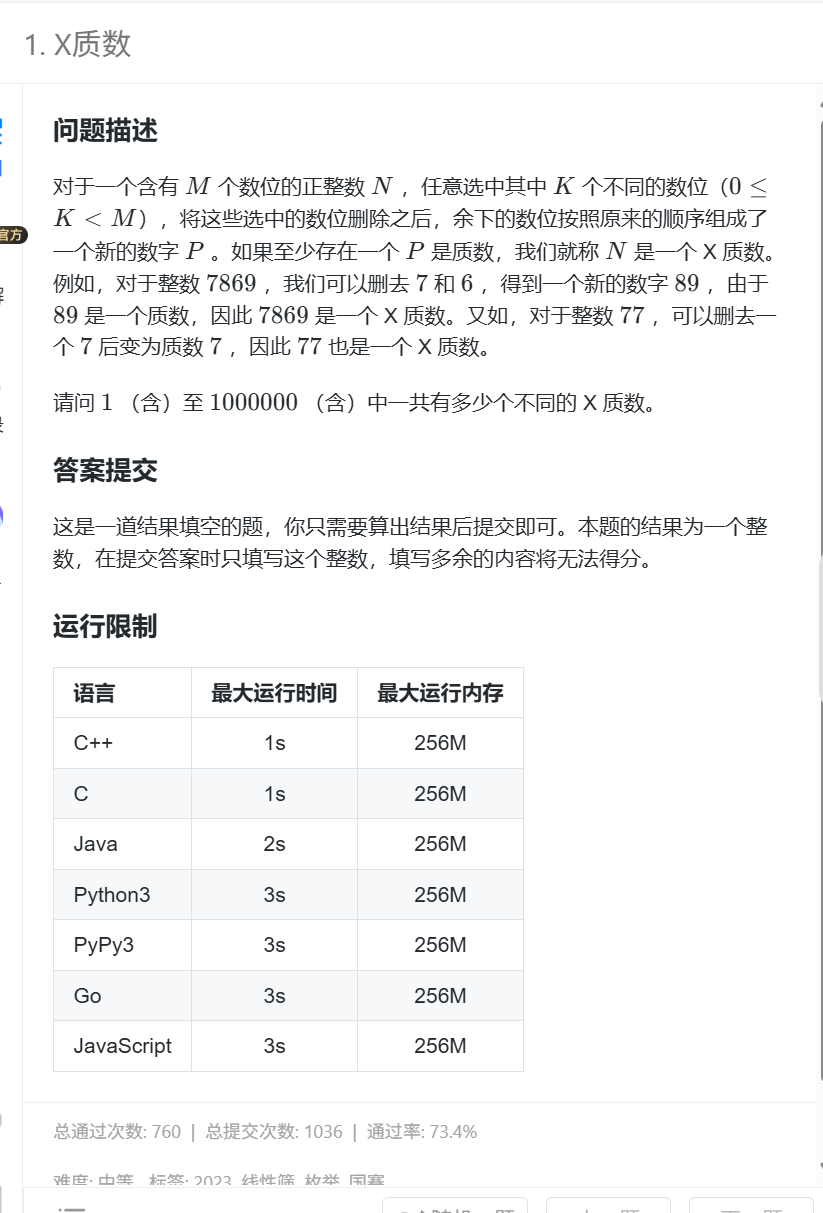
package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.ArrayList;public class X质数 {public static void main(String[] args) {//线性筛把质数筛出来int[] minp = new int[1000001];ArrayList<Integer> prime = new ArrayList<>();boolean[] isp = new boolean[1000001];for (int i = 2; i <= 1000000; i++) {if(minp[i] == 0){prime.add(i);}for (int pp : prime){if(pp * i > 1000000){break;}minp[i * pp] = pp;if(minp[i] == pp){break;}}}for (int pp : prime){isp[pp] = true;}int ans = 0;//二进制遍历判断是否为质数for (int i = 1; i < 1000001; i++) {String s = i + "";int ls = s.length();for (int j = 1; j < Math.pow(2,ls); j++) {String er = Integer.toBinaryString(j);int ler = er.length();String dudu = "";for (int k = ler - 1; k >= 0; k--) {if(er.charAt(k) == '1'){dudu = s.charAt(k + ls -ler) + dudu;}}int now = Integer.parseInt(dudu);if(isp[now]){ans++;break;}}}System.out.println(ans);}
}求解组合数

package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.Scanner;public class 求解组合数 {static int mod = 1000000007;static long[] ni;static long[] jie;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);//求阶乘jie = new long[10000001];jie[0] = 1;for (int i = 1; i < 10000001; i++) {jie[i] = (jie[i-1] * i) % mod;}//求逆元ni = new long[10000001];ni[0] = 1;for (int i = 1; i < 10000001; i++) {ni[i] = niyuan(jie[i]);}int q = scanner.nextInt();for (int i = 0; i < q; i++) {int n = scanner.nextInt();int m = scanner.nextInt();System.out.println((((jie[n] * ni[m]) % mod) * ni[n-m]) % mod);}}//快速乘法幂求逆元static long niyuan(long x){long res = 1;int y = mod - 2;while (y > 0){if((y & 1) == 1){res = (res * x) % mod;}y>>= 1;x = (x * x) % mod;}return res;}
}欧拉降幂(乘积幂次)

package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.Scanner;public class 乘积幂次_欧拉降幂 {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();int mod = 1000000007;//求幂次long fm = 1;for (int i = 1; i <= m; i++) {fm = (fm * i) % (mod - 1);}//快速乘法幂long en = 1;int x = n;long y = fm;while (y > 0){if((y & 1) == 1){en = (en * x) % mod;}y >>= 1;x = (x * x) % mod;}System.out.println(en);}
}乘法逆元

//package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int t = scanner.nextInt();int mod = 1000000007;for (int i = 0; i < t; i++) {int n = scanner.nextInt();long x = n;int y = mod - 2;long res = 1;//快速乘法幂while (y > 0){if((y & 1) == 1){res = (res * x) % mod;}y >>= 1;x = (x * x) % mod;}System.out.println(res);}}
}最小质因子之和

模版
package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.ArrayList;
import java.util.Scanner;public class 最小质因子之和 {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int[] minp = new int[20000001];ArrayList<Integer> Prime = new ArrayList<>();for (int i = 2; i < 20000001; i++) {if(minp[i] == 0){Prime.add(i);minp[i] = i;}for (int pp : Prime){if(pp * i > 20000000){break;}minp[pp*i] = pp;if(minp[i] == pp){break;}}}//求前缀和for (int i = 2; i < 20000001; i++) {minp[i] = minp[i-1] + minp[i];}int t = scanner.nextInt();for (int i = 0; i < t; i++) {int n = scanner.nextInt();System.out.println(minp[n]);}}
}package com.js.datastructure.recursion.蓝桥.国特训练营.数论;import java.util.ArrayList;public class 模版 {static ArrayList<Integer> prime;static int[] minp;public static void main(String[] args) {}//快速乘法幂//有取余的时候都取余static long fast(int x, int y){long res = 1;while (y > 0){if((y & 1) == 1){res = res * x;}y>>=1;x = x * x;}return res;}//线性筛static void shai(){for (int i = 2; i < minp.length; i++) {if(minp[i] == 0){prime.add(i);minp[i] = i;}for (int pp : prime){if(pp * i >= minp.length){break;}minp[pp*i] = pp;if(minp[i] == pp){break;}}}}//欧拉函数:就是小于这个数和他互质数的个数,质数为n-1static int oula(int x){int res = x;for (int i = 2; i <= x / i; i++) {if(x % i == 0){res = res / i * (i-1);while (x % i == 0){x/=i;}}}if(x > 1){res = res / x * (x-1);}return res;}//求逆元//模数为质数是,逆元为a^m-2 % m ,用快速乘法幂//大组合数
}