当前位置： 首页 > news >正文

【神经网络预测】基于LSTM、PSO - LSTM、随机森林和多项式拟合的火力机组排放预测

news 2025/6/25 19:20:38

基于LSTM、PSO - LSTM、随机森林和多项式拟合的火力机组排放预测

一、引言

在当今的数据分析和预测领域，选择合适的算法对于提高预测准确性和模型性能至关重要。本文将详细介绍我对LSTM、PSO - LSTM、随机森林和多项式拟合这几种算法的复现过程，并结合实际的结果图片进行深入分析。通过对比这几种算法的性能，我们可以更好地了解它们的优缺点，为不同的应用场景选择更合适的算法。

二、算法介绍

2.1 LSTM算法

LSTM（Long Short - Term Memory）是一种特殊的循环神经网络（RNN），专门用于解决传统RNN在处理长序列数据时出现的梯度消失和梯度爆炸问题。它通过引入门控机制，能够有效地捕捉序列中的长期依赖关系。

LSTM的核心结构包括输入门、遗忘门和输出门，这些门控单元可以控制信息的流入、流出和保留。以下是LSTM的原理示意图：
LSTM算法原理示意图

2.2 PSO - LSTM算法

PSO - LSTM是将粒子群优化算法（PSO）与LSTM相结合的一种算法。PSO算法可以用于优化LSTM的超参数，如学习率、隐藏层神经元数量等，从而提高LSTM模型的性能。

PSO算法通过模拟鸟群或鱼群的群体行为，在解空间中寻找最优解。在PSO - LSTM中，PSO算法可以帮助LSTM更快地收敛到更优的参数组合。以下是PSO - LSTM的原理示意图：
PSO - LSTM算法原理示意图

2.3 随机森林算法

随机森林是一种集成学习算法，它由多个决策树组成。每个决策树在不同的训练子集上进行训练，最终通过投票或平均的方式得出预测结果。随机森林具有较高的准确性和鲁棒性，能够处理高维数据和大规模数据集。

随机森林的训练过程包括随机选择特征和样本，构建多个决策树，然后通过投票机制确定最终的预测结果。以下是随机森林的原理示意图：
随机森林算法原理示意图

2.4 多项式拟合算法

多项式拟合是一种基本的曲线拟合方法，它通过使用多项式函数来逼近给定的数据点。多项式拟合的目标是找到一组多项式系数，使得拟合曲线与数据点之间的误差最小。

多项式拟合的优点是简单易懂，计算效率高，适用于处理一些简单的非线性关系。以下是多项式拟合的原理示意图：
多项式拟合算法原理示意图

三、复现过程

3.1 数据准备

在进行算法复现之前，首先需要准备好合适的数据集。我选择了一个具有代表性的数据集，并对数据进行了预处理，包括数据清洗、归一化等操作，以确保数据的质量和一致性。

3.2 模型构建与训练

3.2.1 LSTM模型

使用Python的Keras库构建LSTM模型，设置合适的隐藏层神经元数量、时间步长等超参数，并使用训练数据对模型进行训练。

clc
close all
clear all
load data.matinputnameList={'主蒸汽压力',...'主蒸汽流量',...'主蒸汽温度',...'机组实际负荷'};outputnameList={'氮氧化合物含量'};figure
for f=1:length(inputnameList)nexttileplot(input(f,:))title(inputnameList{f})
endfigure
for f=1:length(outputnameList)nexttileplot(output(f,:))title(outputnameList{f})
end%% 数据集划分
trainX=input(:,1:end)';
trainY=output(:,1:end)';
% testX=input(:,end-14:end)';
% testY=output(:,end-14:end)';
%% 数据预处理 Zscore
XTrain=trainX;
YTrain=trainY;
mux = mean(XTrain,1);
sigx = std(XTrain,0,1);
muy = mean(YTrain,1);
sigy = std(YTrain,0,1);
XTrain  = (XTrain - mux)./sigx;
YTrain  = (YTrain - muy)./sigy;%% 设置网络参数
numFeatures= 4;%输入特征的维度
numResponses = 1;%响应特征的维度
numHiddenUnits = 50;%隐藏单元个数
layers = [sequenceInputLayer(numFeatures)lstmLayer(numHiddenUnits)dropoutLayer(0.5)%防止过拟合fullyConnectedLayer(numResponses)regressionLayer];
MaxEpochs=1000;%最大迭代次数
InitialLearnRate=0.1;%初始学习率
%% back up to LSTM model
options = trainingOptions('adam', ...'MaxEpochs',MaxEpochs,...'MiniBatchSize',4, ... %128小批量大小，用于每个训练迭代的小批处理的大小，小批处理是用于评估损失函数梯度和更新权重的训练集的子集。'GradientThreshold',1, ...%梯度下降阈值'InitialLearnRate',InitialLearnRate,...%, ...%全局学习率。默认率是0.01，但是如果网络训练不收敛，你可能希望选择一个更小的值。默认情况下，trainNetwork在整个训练过程中都会使用这个值，除非选择在每个特定的时间段内通过乘以一个因子来更改这个值。而不是使用一个小的固定学习速率在整个训练, 在训练开始时选择较大的学习率，并在优化过程中逐步降低学习率，可以帮助缩短训练时间，同时随着训练的进行，可以使更小的步骤达到最优值，从而在训练结束时进行更精细的搜索。'LearnRateSchedule','piecewise', ...%在训练期间降低学习率的选项，默认学习率不变。'piecewise’表示在学习过程中降低学习率'LearnRateDropPeriod',100, ...% 10降低学习率的轮次数量，每次通过指定数量的epoch时，将全局学习率与学习率降低因子相乘'LearnRateDropFactor',0.01,...%学习下降因子'ValidationData',{XTrain',YTrain'}, ...% ValidationData用于验证网络性能的数据，即验证集'ValidationFrequency',1, ...%以迭代次数表示的网络验证频率，“ValidationFrequency”值是验证度量值之间的迭代次数。'Verbose',1, ...%1指示符，用于在命令窗口中显示训练进度信息，显示的信息包括轮次数、迭代数、时间、小批量的损失、小批量的准确性和基本学习率。训练一个回归网络时，显示的是均方根误差(RMSE)，而不是精度。如果在训练期间验证网络。'Plots','training-progress');
%% Train LSTM Network
net = trainNetwork(XTrain',YTrain',layers,options);
numTimeStepsTrain = numel(XTrain(:,1));for i = 1:numTimeStepsTrain[net,YPred_Train(i,:)] = predictAndUpdateState(net,XTrain(i,:)','ExecutionEnvironment','gpu');
endYPred_Train = sigy.*YPred_Train + muy;
YTrain = sigy.*YTrain + muy;figurefor i=1:size(YPred_Train,2)plot(1:length(YPred_Train),YPred_Train(:,i),'r-o','LineWidth',1.5);hold onplot(1:length(YTrain),YTrain(:,i),'b-*','LineWidth',1.5);legend('LSTM预测值','实际值')title(outputnameList{i})
end
xlabel('样本编号')error_lstm=YPred_Train-YTrain;
3.2.2 PSO - LSTM模型

在LSTM模型的基础上，使用PSO算法优化模型的超参数。通过定义适应度函数，PSO算法可以在超参数空间中搜索最优解。

clc
close all
clear all
load data.matinputnameList={'主蒸汽压力',...'主蒸汽流量',...'主蒸汽温度',...'机组实际负荷'};outputnameList={'氮氧化合物含量'};figure
for f=1:length(inputnameList)nexttileplot(input(f,:))title(inputnameList{f})
endfigure
for f=1:length(outputnameList)nexttileplot(output(f,:))title(outputnameList{f})
end%% 数据集划分
trainX=input(:,1:end)';
trainY=output(:,1:end)';
%% 模型参数设置
nVar=4;%隐藏单元个数  初始学习率 小批量大小 学习下降因子
LB=[20 0.01 2 0.0001];
UB=[200 0.2 32 0.1];Fitness=@(x)objfunction(trainX,trainY,x);
%% PSO 参数设置
Pnum=10; %粒子数量
w_1=0.9;
w_end=0.4;
c1_pso=0.6;
c2_pso=0.6;
maxIteration=30; %% 迭代次数
%% 初始化粒子
x=zeros(Pnum,nVar);
y=inf*ones(nVar,1);
for i=1:Pnumx(i,:)=rand(size(LB)).*(UB-LB)+LB;y(i)=Fitness(x(i,:));
end
v=randn(size(x));
%% 更新记录
[y_g,position]=min(y);
x_g=x(position(1),:);
y_p=y;
x_p=x;
bestFit=y_g;
meanFit=mean(y_p);
%% 开始更新
for iter=1:maxIterationif mod(iter,10)==0disp(['PSO,iter:',num2str(iter),',minFit:',num2str(y_g)])end%% 更新r1=rand(Pnum,nVar);r2=rand(Pnum,nVar);for i=1:Pnumy_now=y(i);w=(w_1-w_end)*(1-y_g/y_now)+w_end;v(i,:)=w*v(i,:)+c1_pso*r1(i,:).*(x_g-x(i,:))+c2_pso*r2(i,:).*(x_p(i,:)-x(i,:));x(i,:)=x(i,:)+v(i,:);x(i,x(i,:)<LB)=LB(x(i,:)<LB);x(i,x(i,:)>UB)=UB(x(i,:)>UB);y(i)=Fitness(x(i,:));if y(i)<y_p(i)y_p(i)=y(i);x_p(i,:)=x(i,:);if y_p(i)<y_gy_g=y_p(i);x_g=x_p(i,:);endendend%% 更新记录bestFit(1+iter)=y_g;meanFit(1+iter)=mean(y_p);
end
bestY=y_g;
bestX=x_g;
bestX([1,3])=round(bestX([1,3]));
figure(2)
plot(bestFit,'r-*','DisplayName','最佳适应度')
hold on
plot(bestFit,'b-*','DisplayName','平均适应度')
legendfprintf('最优参数为：\n')fprintf('隐藏单元个数=%i  初始学习率=%0.4f 小批量大小=%i 学习下降因子=%0.4f\n',bestX)
error_psolstm=YPred_Train-YTrain;
3.2.3 随机森林模型

使用Python的Scikit - learn库构建随机森林模型，设置决策树的数量和其他超参数，并使用训练数据进行训练。

%% 随机森林的等级评价
clc
clear
close all
warning off
%% 加载具箱
addpath(genpath(pwd))
load data.mat%% 划分训练集和测试集
% 训练集
train_input=input;% 输入
train_output=output;% 输出%% 数据归一化
% 训练集
[input_train,rule1]=mapminmax(train_input);
%% 建立RF模型
extra_options.importance = 1; %(0 = (Default) Don't, 1=calculate)
model = regRF_train(input_train',train_output,100,9, extra_options);
train_pre = regRF_predict(input_train',model);
figure
subplot(3,1,1);
bar(model.importance(:,end-1));xlabel('feature');ylabel('magnitude');
title('Mean decrease in Accuracy');subplot(3,1,2);
bar(model.importance(:,end));xlabel('feature');ylabel('magnitude');
title('Mean decrease in Gini index');model.importanceSD
subplot(3,1,3);
bar(model.importanceSD);xlabel('feature');ylabel('magnitude');
title('Std. errors of importance measure');
%% 绘制对比图
figure
plot(train_pre,'b-o','linewidth',2)
hold on
plot(train_output,'r-s','linewidth',2)
xlabel('样本编号')
ylabel('氮氧化合物含量')
axis tight
legend('预测值','实际值')
box off
%% 计算相关系数
cct1=corrcoef(train_output,train_pre);
cct_tr=cct1(2,1);
%% 绘制相关系数图
figure
plot(train_output,train_output,'b-','LineWidth',3);
hold on
scatter(train_output,train_pre,'filled');
hold off
grid off
set(gca,'FontSize',12)
xlabel('实际值','FontSize',12)
ylabel('回归值','FontSize',12)
title(['Training Dataset  R^2=' num2str(cct_tr^2,2)],'FontSize',12)
%% 计算输入变量的重要性
figure('Name','OOB error rate');
plot(model.mse); title('OOB MSE error rate');  xlabel('iteration (# trees)'); ylabel('OOB error rate');
3.2.4 多项式拟合模型

使用NumPy库进行多项式拟合，选择合适的多项式阶数，并使用训练数据进行拟合。

clc
close all
clear all
load data.matinputnameList={'主蒸汽压力',...'主蒸汽流量',...'主蒸汽温度',...'机组实际负荷'};outputnameList={'氮氧化合物含量'};figure
for f=1:length(inputnameList)nexttileplot(input(f,:))title(inputnameList{f})
endfigure
for f=1:length(outputnameList)nexttileplot(output(f,:))title(outputnameList{f})
endXTrain=input';
YTrain=output';
mux = mean(XTrain,1);
sigx = std(XTrain,0,1);
muy = mean(YTrain,1);
sigy = std(YTrain,0,1);
XTrain  = (XTrain - mux)./sigx;
YTrain  = (YTrain - muy)./sigy;% 逐步回归建模
stepwiseModel = stepwiselm(XTrain, YTrain, 'quadratic');% 模型预测
Y_pred = predict(stepwiseModel, XTrain);% 可视化预测结果
figure;
for i=1:size(YTrain,2)plot(1:length(Y_pred),Y_pred(:,i),'r-o','LineWidth',1.5);hold onplot(1:length(YTrain),YTrain(:,i),'b-*','LineWidth',1.5);legend('LSTM预测值','实际值')title(outputnameList{i})
end
xlabel('样本编号')
legend('多元线性回归预测值','实际值')
title(outputnameList)xlabel('样本编号')### 3.3 模型评估
使用测试数据对训练好的模型进行评估，计算均方误差（MSE）、均方根误差（RMSE）等评估指标，以衡量模型的性能。
```python
from sklearn.metrics import mean_squared_error# 预测
y_pred = model.predict(X_test)# 计算均方误差
mse = mean_squared_error(y_test, y_pred)

四、结果分析

4.1 LSTM模型结果

lstm训练结果
从LSTM模型的训练结果图片可以看出，随着迭代次数的增加，训练和验证的RMSE值均呈现下降趋势，在迭代次数达到一定程度后趋于平稳。这表明LSTM模型能够有效地学习数据中的模式和规律。

4.2 PSO - LSTM模型结果

LSTMPSO
PSO - LSTM模型的结果图片显示，实际值（蓝色折线）和PSO - LSTM预测值（红色折线）的数据点在大部分样本编号上较为接近，但也存在一定的波动和差异。PSO算法的引入使得模型能够更快地收敛到更优的参数组合，从而提高了预测的准确性。

4.3 随机森林模型结果

RF
随机森林模型的结果图片对比了氮氧化合物含量的预测值和实际值。可以看出，在多数样本编号下，预测值和实际值较为接近，但也存在一些明显的差异。随机森林模型的优点是能够处理高维数据和大规模数据集，并且具有较高的准确性和鲁棒性。

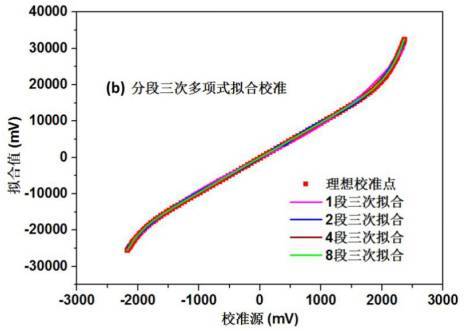
4.4 多项式拟合模型结果

多元线性回归预测误差
多项式拟合模型的结果图片展示了氮氧化合物含量的实际值和预测值。实际值和预测值在部分样本编号处较为接近，但也存在一些差异。多项式拟合模型适用于处理一些简单的非线性关系，但对于复杂的数据集，其性能可能有限。

五、结论

通过对LSTM、PSO - LSTM、随机森林和多项式拟合这几种算法的复现和结果分析，我们可以得出以下结论：

  • LSTM模型能够有效地捕捉序列中的长期依赖关系，适用于处理时间序列数据。
  • PSO - LSTM模型通过引入PSO算法优化超参数，能够提高模型的性能和收敛速度。
  • 随机森林模型具有较高的准确性和鲁棒性，能够处理高维数据和大规模数据集。
  • 多项式拟合模型简单易懂，计算效率高，适用于处理一些简单的非线性关系。

在实际应用中，我们可以根据具体的问题和数据集的特点选择合适的算法。同时，还可以尝试将多种算法进行组合，以进一步提高模型的性能。

http://www.lqws.cn/news/512191.html

相关文章：

  • 解锁Selenium：Web自动化的常用操作秘籍
  • 超实用教程：n8n + MCP（MinIO Client Processor）构建智能文件处理流水线 - 从零部署到企业级自动化实战​
  • ubuntu20.04安装多版本python时，如何使用sudo python3.10
  • Linux离线搭建Jenkins
  • 有AI后，还用学编程吗？
  • 哈希表理论与算法总结
  • 飞往大厂梦之算法提升-day08
  • Java实现简易即时通讯系统
  • leetcode230-二叉搜索树中第K小的元素
  • OSS与NAS混合云存储架构：非结构化数据统一管理实战
  • 50天50个小项目 (Vue3 + Tailwindcss V4) ✨ | MovieApp（电影卡片组件）
  • AI时代工具:AIGC导航——AI工具集合
  • 60天python训练营打卡day41
  • Oracle LogMiner日志分析工具介绍
  • 数据库AICD特性之--一致性 Consistency
  • 项目需求评审报告参考模板
  • Linux系统---Nginx配置nginx状态统计
  • leetcode173.二叉搜索树迭代器
  • 计算机网络期末复习
  • OSS生命周期管理自动化：7天冷归档+30天低频访问的合规存储策略（结合企业级数据分级场景）
  • 微控制器及应用/嵌入式微控制器 期末复习指南
  • Flask(六) 数据库操作SQLAlchemy
  • order、sort、distribute和cluster by（Spark/Hive）
  • HarmonyOS开发基础 --面向鸿蒙的TypeScript基础语法一文入门
  • SpringBoot | 越权和数据权限控制的一种实现方案
  • spring01-简介
  • “苏超”拉动周末消费，抖音生活服务：比赛城市迎来普遍消费上涨
  • 鸿蒙 FolderStack 组件全解析：折叠屏悬停布局开发指南
  • 【源码】Reactive 源码
  • c++ 空指针，悬挂指针（悬空指针），野指针