不同视角理解三维旋转
在二维空间中,绕任意点旋转可以分解为:
1)平移旋转点到原点,2)绕原点旋转,3)逆平移旋转点;
可用矩阵表示为

,
其中,

表示绕原点旋转

,
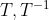
为平移矩阵。
在三维空间中绕任意轴旋转一个对象,可以分解为分别绕不同轴旋转一定角度。
1 绕三维坐标轴旋转
设 x,y,z 为三个正交方向上的单位向量,将他们构成三维空间坐标需要满足以下叉乘关系:
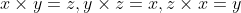
;
定义绕各个坐标轴旋转方向如下图:
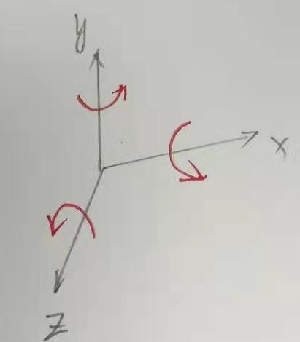
当任意点绕 Z 轴旋转时,该点在 Z 轴上坐标保持不变,在 X,Y 轴上坐标轴上退化为二维旋转,如下图所示:
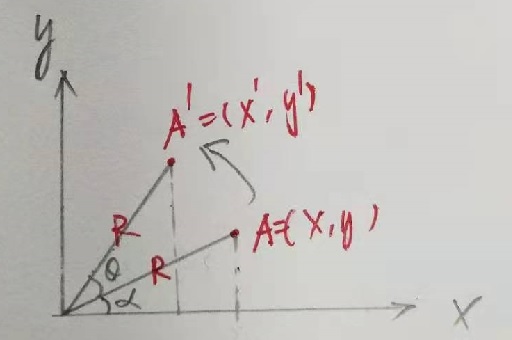
由

得

,
由

得

,
最终得:

,其中矩阵变换表示为:

;
同理, 绕 X 轴旋转表示为:

,绕 Y 轴旋转表示为:

。
当对任意点旋转
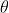
后再旋转
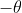
,该点回到原始位置,则旋转矩阵
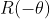
是旋转矩阵

得逆矩阵,观察以上旋转矩阵可知

。
2 绕过原点任意单位向量轴旋转
当旋转轴为过原点任意轴时,可使用如下方案旋转:
1)旋转对象使得旋转轴与某一坐标轴重合;
2)绕该坐标轴旋转;
3)使用逆旋转使旋转轴回到原始方向;
使用矩阵表示为:
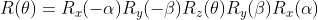
。
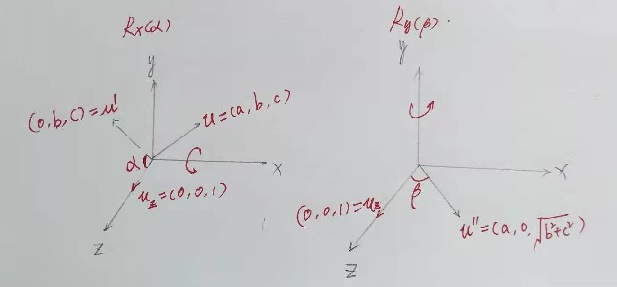
如上图所示,u=(a,b,c) 为任意过原点旋转轴,
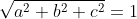
。要旋转 u 使其与 z 轴重合,首先需将 u 轴旋转到 xz 平面。
将 u 投影到 yz 平面得
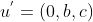
,在 yz 平面上将

旋转 到 z 轴的旋转角等于将 u 绕 x 轴旋转到 xz 平面。
根据余弦定理得:

。
利用向量叉乘求正弦:
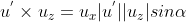
,
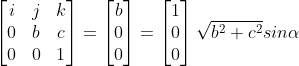
,
求解得:
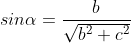
。这里不使用

求解是因为该公式无法确定计算结果符号。
使用矩阵形式表示 u 绕 x 轴旋转
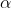
:

,旋转后向量为:

。
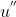
绕 y 轴旋转到 z 轴上的旋转角余弦为:

。
利用向量叉乘求正弦:

,

,

。
使用矩阵形式表示
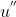
绕 y 轴旋转
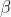
:

。
当将任意单位坐标做旋转到与 z 轴重合后,使用以下矩阵完成真实旋转:

。
然后使用逆旋转矩阵还原原始坐标(逆旋转矩阵为对应旋转矩阵的转置矩阵),实现绕任意过原点单位向量旋转。
3 罗德里格斯公式
使用罗德里格斯公式,同样可以实现绕过原点任意单位向量旋转,详细讲解在 使用罗德里格斯公式描述三维旋转_rodriguez formula的引用-CSDN博客。
该方法最终推导出了旋转矩阵为:
![]()
,

。
理论上来说,以上两种方案推导出的旋转矩阵应该是一致的(旋转轴与旋转角度一致情况下)。
4 引入平移
当旋转轴不过原点时,可以引入平移矩阵实现绕任意轴旋转。
假设旋转轴过点

,
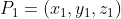
,

,
首先构造单位长度旋转轴向量为:

,
构造平移矩阵为:
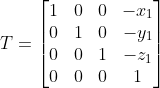
,
旋转矩阵

被改写为:
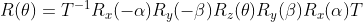
,
旋转轴为以上单位旋转向量,从而实现了绕任意轴旋转。
在罗德里格斯公式中,采用同样方式构造绕任意轴旋转矩阵为:

。
5 四元数描述旋转
1)四元数概念
四元数是复数到高维扩充,定义为

,
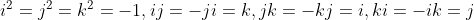
。
将四元数表示成向量

,
定义四元数加法为
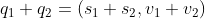
,
等价于

。
定义四元数乘法为

。
由于四元数平方和为
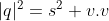
,可定义四元数的逆为
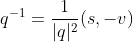
,使得
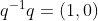
成立。
2)描述旋转轴为过原点任意单位向量的旋转
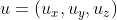
为旋转轴单位向量,定义

,
则任意点 p = (x,y,z) 被描述为
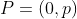
,旋转后点为

,
使用公式

可计算出 p 点旋转后坐标

。
使用四元数计算规则可得
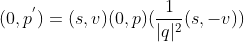
,
由于
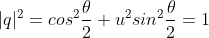
,有
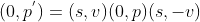
,

。
引入向量 v 的叉积矩阵
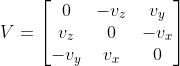
,上式可改写为:

,实现 p 到

旋转变换。
3)与罗德里格斯公式关系
令旋转轴为单位向量(x,y,z),旋转角度为
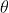
,旋转四元数定义为

;
根据三角函数有
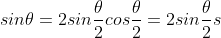
,
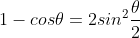
,
罗德里格斯公式改写为
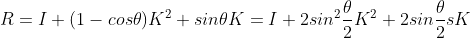
,
由于
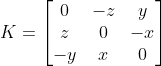
,可定义

,
进一步改写罗德里格斯公式
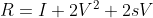
,
最终整理结果为
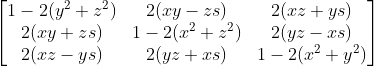
;
将
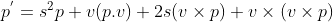
整理成矩阵形式,其结果与罗德里格斯整理矩阵一致,因此验证了两种方式是一致的。
