卡特兰数简单介绍

卡特兰数（Catalan Number）是组合数学里的一组数列，在多种 “有约束的排列、路径、结构计数” 场景中频繁出现，和栈的出栈序列计数是典型关联。

一、定义与公式

• 定义：卡特兰数 \(C_n\) 用于计数满足特定 “不交叉、不冲突” 约束的组合情况，是一种递归定义的数列。
• 公式：
  1. 递归式：（通过子问题组合推导）。
  2. 闭合式（常用）：（) 是组合数，表示从 2n 个元素选 n 个的方式数，再通过 约束非法情况）

二、和栈的关联（出栈序列计数）

当有 n 个元素依次进栈时，合法出栈序列的数量恰好是第 n 个卡特兰数 。

核心逻辑： 每次出栈需满足 “进栈数 ≥ 出栈数”（否则栈空无法出栈），这等价于卡特兰数的 “不跨越对角线” 约束。

比如 n=3（元素 a,b,c 依次进栈）：

• 合法出栈序列共 种：abc、acb、bac、bca、cba（对应卡特兰数递推）。

三、其他典型应用场景

卡特兰数不止用于栈，还能解决很多 “有隐含约束的计数问题”，常见场景：

1. 括号匹配

• 问题：n 对括号（( 和 )），有多少种合法的匹配方式？
• 解释：每一步新增括号需满足 “左括号数 ≥ 右括号数”，等价于栈的 “进栈数 ≥ 出栈数”，结果为 。

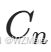2. 凸多边形三角划分

• 问题：一个凸 (n+2) 边形，用 n-1条不相交的对角线，能划分成多少个三角形？
• 解释：选一条边作为基准，递归分割左右子多边形，符合卡特兰数的递归结构，结果为 \(C_n\)。

3. 路径计数（不跨越对角线）

• 问题：从 (0,0)走到 (n,n)，只能向右或向上走，且不越过对角线 y=x，有多少种路径？
• 解释：每一步向右（类似进栈）或向上（类似出栈），约束 “向右步数 ≥ 向上步数”，结果为 \。

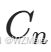四、本质：“合法约束” 的计数模型

卡特兰数的核心是 **“避免非法前置” 的组合计数 **：所有操作需满足 “某类操作数（如进栈、左括号、向右走）始终 ≥ 另一类操作数（如出栈、右括号、向上走）”。这种约束让卡特兰数成为解决 “对称操作计数” 问题的通用工具。

简单说，卡特兰数就是专门用来数 “有顺序约束的组合情况” 的数学工具，栈的出栈序列只是其中一个经典例子